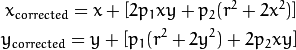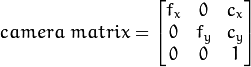Merhabalar, bu yazı Opencv resmi sitesinde bulunan buradaki yazının çevirisidir. Hızlıca giriş yapalım.
Bu bölümde,
- Kameradaki bozulmalar, kamera iç ve dış parametreleri vb. hakkında bilgi edineceğiz.
- Bu parametreleri bulmayı, görüntüdeki bozukluğu gidermeyi vb. öğreneceğiz.
Bugünün ucuz iğne deliği kameralardan alınan görüntülerde çok fazla bozulma meydana geldiği malumdur. Tür olarak radyal bozulma ve teğetsel bozulma şeklinde iki ana bozulma türü vardır.
Radyal bozulmanın etkisi sonucu düz çizgiler kavisli bir görünüm alır. Etkisi görüntünün merkezinden uzaklaştıkça daha da artar. Örneğin, bir satranç tahtasının iki kenarının kırmızı çizgilerle işaretlendiği bir resim aşağıda gösterilmiştir. Görüldüğü gibi sınırın düz bir çizgi olmadığını ve çizilen kırmızı çizgi ile eşleşmediğini görebilirsiniz. Beklenen tüm düz çizgiler şişmiş. Daha fazla ayrıntı için Distorsiyon(optik) adresini ziyaret edebilirsiniz.
Bu bozulma şu matematik denklemleriyle düzeltilir:
Benzer şekilde bir başka bozulma da, görüntünün geldiği merceğin görüntüleme düzlemine tam paralel olarak hizalanmadığı için meydana gelen teğetsel bozulmadır. Dolayısıyla görüntüdeki bazı alanlar beklenenden daha yakın görünebilir. Bu bozulma da şu denklemlerle düzeltilir:
Kısacası, aşağıdaki şekilde verilen bozulma katsayıları olarak bilinen beş parametreyi bulmamız gerekir:
Buna ek olarak, kameranın iç ve dış parametreleri gibi birkaç parametre daha bulmamız gerekiyor. İçsel parametreler kameraya özgü olup odak uzaklığı (f_x, f_y) ve optik merkezi (c_x, c_y) vb. gibi bilgileri içerir. Ayrıca kamera matrisi olarak da adlandırılır. Yalnızca kameraya bağlıdır, bu yüzden hesaplandıktan sonra gelecekteki hesaplamalar için saklanıp daha sonra da kullanılabilir. 3×3’lük bir matris olarak ifade edilir:
Dış parametreler, üç boyuttaki bir noktanın koordinatlarını bir koordinat sistemine çeviren dönme ve öteleme vektörlerine karşılık gelir.
Bu gibi stereo uygulamalarda önce bu bozulmaların düzeltilmesi gerekir. Tüm bu parametreleri bulmak için yapmamız gereken, bilinen bir desenin birkaç örnek imajını alıp işleme koymak olacaktır(örneğin satranç tahtası). Şimdi seçtiğimiz desende bazı özel noktalar bulduk diyelim (satranç tahtasında kare köşeler gibi). Bu özel noktaların koordinatlarını gerçek (dünyadaki) uzayda biliyoruz ve görüntüdeki koordinatlarını da biliyoruz. Bu verileri kullanarak arka planda bazı matematiksel problemler bilgisayar yardımıyla çözülüyor ve biz de bozulma katsayılarını elde ediyoruz. Bütün hikayenin özeti bu. Daha iyi sonuçlar için, en az 10 test desenine ihtiyacımız var.
Kod kısmı
Yukarıda belirtildiği gibi, kamera kalibrasyonu için en az 10 test desenine ihtiyacımız var. OpenCV, içinde bazı satranç tahtası görüntü örneğiyle birlikte yüklenir(bkz. samples/cpp/left01.jpg – left14.jpg), biz de bunları kullanacağız. Anlamanız için, bir satranç tahtasının sadece bir görüntüsünü düşünün. Kamera kalibrasyonu için gereken önemli giriş verileri, bir dizi 3B gerçek dünyaki noktası ve buna karşılık gelen 2B görüntü noktalarıdır. 2B görüntü noktalarını da görüntüden kolayca bulabiliriz. (Bu görüntü noktaları, satranç tahtasındaki iki siyah karenin birbirine temas ettiği yerlerdir.)
Peki ya gerçek dünyadaki 3B noktaları? Bu görüntüler statik bir kamera tarafından ve satranç tahtalarının farklı yerlere ve yönlere yerleştirilmiştir hallerinden alınmıştır. Bu yüzden (X, Y, Z) değerlerini bilmemiz gerekir. Ancak basitlik açısından, satranç tahtasının sabit x-y düzleminde tutulduğunu, (her zaman Z = 0 ) ve kameranın uygun şekilde hareket ettiğini söyleyebiliriz. Bu değerlendirme sadece X ve Y değerlerini bulmamıza yardımcı olmaktadır. Şimdi X, Y değerlerini (0,0), (1,0), (2,0) gibi basitçe noktaların konumunu belirten terimler şeklinde işleme koyabiliriz. Bu durumda elde ettiğimiz sonuçlar satranç tahtasının boyutu ölçeğinde olacaktır. Fakat her bir karenin boyutunu biliyorsak (30 mm gibi), o zaman değerleri (0,0), (30,0), (60,0) şeklinde işleme koyar ve sonuçları mm olarak alırız. (Şuan bu örnekte, bu görüntüleri almadığımızdan kare boyutunu bilmiyoruz, bu yüzden kare boyutu cinsinden işlem yapıyoruz).
3B noktalara nesne noktaları, 2B imge noktalarına da görüntü noktaları denir.
Kurulum
Satranç tahtasındaki deseni bulmak için cv2.findChessboardCorners () metodunu kullanıyoruz. Ayrıca 8×8 ızgara, 5×5 ızgara vb. gibi ne tür bir desen aradığımızı da parametre olarak metoda geçmeliyiz. Bu örnekte 7×6 ızgara kullanıyoruz. (Normalde bir satranç tahtasında 8×8 kare ve 7×7 iç köşe vardır). Desen elde edilirse köşe noktalarını ve retval’i döndürür. Bu köşeler görüntüde sırayla yerleştirilir (soldan sağa, yukarıdan aşağıya).
Köşeleri bulduktan sonra, cv2.cornerSubPix () metodunu kullanarak doğruluk değerini artırabiliriz. Deseni cv2.drawChessboardCorners () kullanarak da çizebiliriz. Tüm bu adımlar aşağıdaki koda dahil edilmiştir:
import numpy as np
import cv2
import glob
# termination criteria
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)
# Arrays to store object points and image points from all the images.
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.
images = glob.glob('*.jpg')
for fname in images:
img = cv2.imread(fname)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
# Find the chess board corners
ret, corners = cv2.findChessboardCorners(gray, (7,6),None)
# If found, add object points, image points (after refining them)
if ret == True:
objpoints.append(objp)
cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
imgpoints.append(corners)
# Draw and display the corners
cv2.drawChessboardCorners(img, (7,6), corners2,ret)
cv2.imshow('img',img)
cv2.waitKey(500)
cv2.destroyAllWindows()
Üzerinde bu kod ile işlem yapılmış desenli bir resim aşağıda gösterilmiştir:
Kalibrasyon
İşte şimdi elimizde obje noktaları ve görüntü noktaları var. Yani kalibrasyon için hazırız. Bunun için Kamera matrisi, bozulma katsayıları, döndürme ve öteleme vektörlerini vb. veren cv2.calibrateCamera () metodunu kullanıyoruz.
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1],None,None)
Çarpıklığı düzeltme
Elde etmeye çalıştığımız şeyi elde ettik. Şimdi bir görüntüyü, şeklini bozmadan elde etmeye çalışalım. Bunun için OpenCV iki yöntemle birlikte geliyor, ikisini de göreceğiz. Ancak bundan önce cv2.getOptimalNewCameraMatrix () metoduyla serbest ölçekleme parametresine dayanan kamera matrisini işleyelim. Ölçekleme parametresi alpha = 0 ise, istenmeyen pikselleri en aza indirerek bozulmamış görüntüyü döndürür. Böylece görüntü köşelerinde bazı pikselleri bile kaldırabilir. Alpha = 1 ise, tüm pikseller bazı ekstra siyah görüntülerle tutulur. Ayrıca sonucu kırpmak için kullanılabilecek bir ROI döndürür. Yeni bir resim çekiyoruz (burada left12.jpg görüntüsü kullanılmıştır).
img = cv2.imread('left12.jpg')
h, w = img.shape[:2]
newcameramtx, roi=cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))
1. cv2.undistort() kullanarak düzeltme
Bu metod en kısa yoldur. Sadece işlevi çağırın ve sonucu kırpmak için yukarıda elde edilen ROI’yi kullanın.
# çarpıklığı düzeltiyoruz
dst = cv2.undistort(img, mtx, dist, None, newcameramtx)
# imajı kırp
x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite('calibresult.png',dst)
2. Remapping kullanarak düzeltme
Bu da uzun yoldur. Öncelikle bozuk görüntüden bozulmamış görüntüye bir mapping metodu kullanın. Ardından remap işlevini kullanın.
# çarpıklığı düzelt
mapx,mapy = cv2.initUndistortRectifyMap(mtx,dist,None,newcameramtx,(w,h),5)
dst = cv2.remap(img,mapx,mapy,cv2.INTER_LINEAR)
# imajı kırp
x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite('calibresult.png',dst)
Her iki yöntem de aynı sonucu verir. Aşağıdaki düzeltilmiş halidir. (Sonucu ilk resimle karşılaştırabilirsiniz)
Sonuç görüntüde artık tüm kenarların düz olduğunu görebilirsiniz.
Artık kamera matrisini ve bozulma katsayılarını, ileride tekrar kullanmak üzere Numpy’ın (np.savez, np.savetxt, vs.) dosya yazma işlevlerini kullanarak kaydedebilirsiniz.
Re-projection Error
Yeniden yansıtma hatası, bulunan parametrelerin tam olarak ne kadar kesin ve doğru olduğu konusunda iyi bir tahmin verir. Bu değer mümkün olduğunca sıfıra yakın olmalıdır. İçsel, bozulma, döndürme ve taşıma matrisleri göz önüne alındığında, önce cv2.projectPoints () işlevini kullanarak nesne noktasını, görüntü noktasına dönüştürürüz. Sonra dönüşümle elde ettiğimiz değer ile köşe bulma algoritmasından gelen değer arasındaki mutlak normu hesaplarız. Ortalama hatayı bulmak için tüm kalibrasyon görüntülerinin hataların aritmetik ortalamasını hesaplıyoruz.
mean_error = 0
for i in xrange(len(objpoints)):
imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
tot_error += error
print "total error: ", mean_error/len(objpoints)